George Stiny: Ice-rays
Artist(s):
Title:
- Ice-rays
Exhibition:
Creation Year:
- 2008
Category:
Artist Statement:
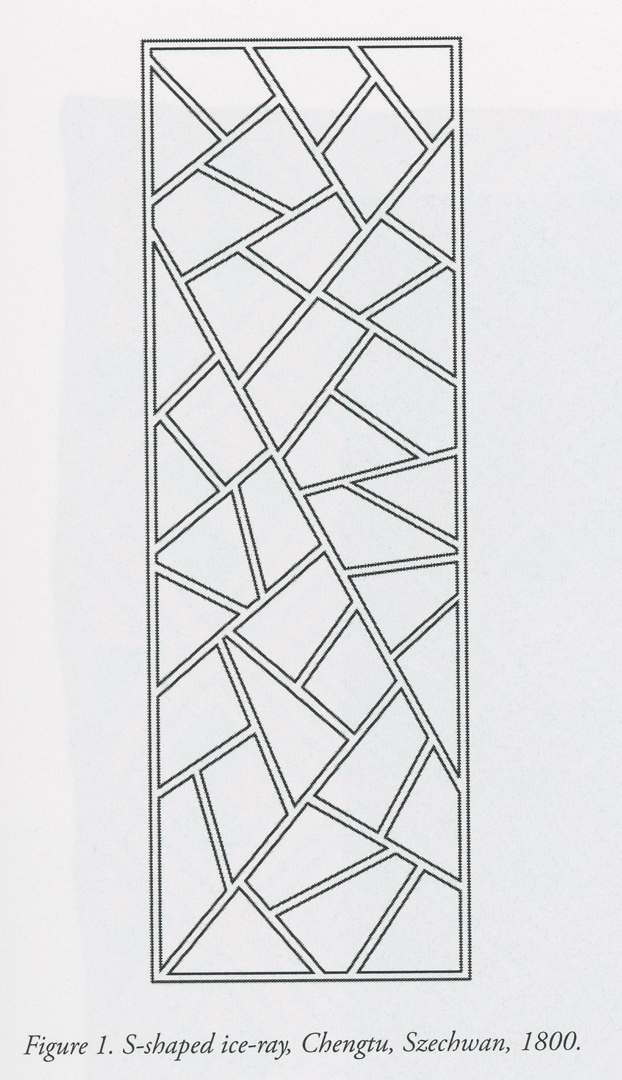
Ice-rays are a kind of traditional Chinese lattice used in ornamental window grilles (figure 1). 1 Ice-rays form irregular patterns that suggest cracking ice on still water — straight lines meet longer lines in myriad ways.
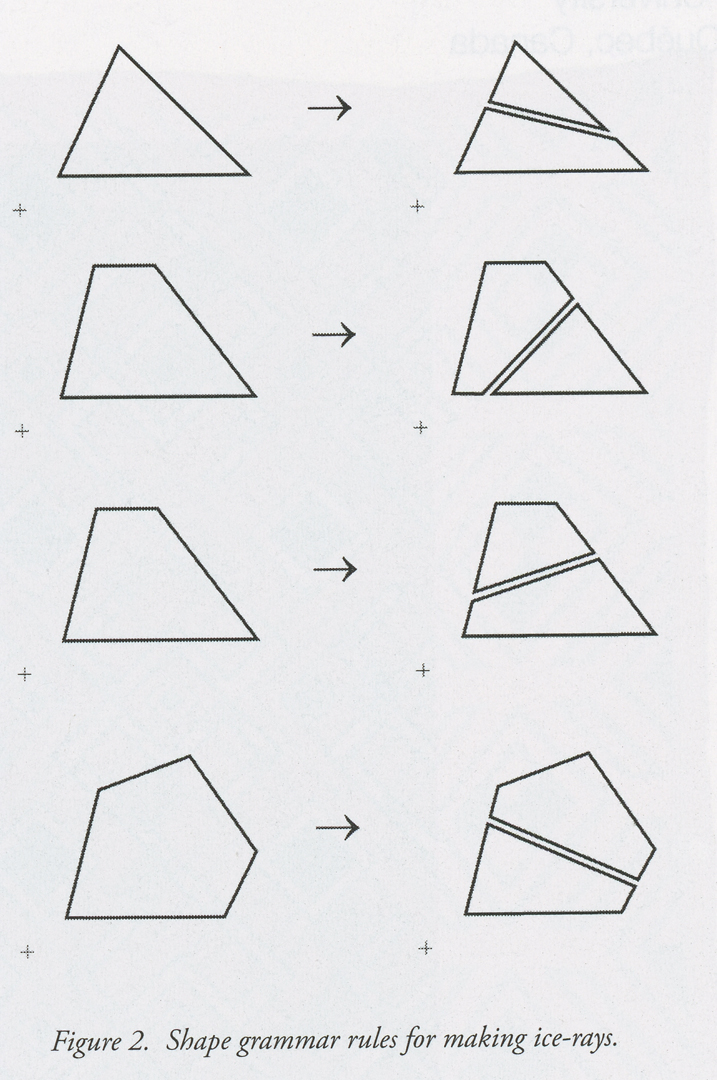
Rules for Ice-rays are easy to define in a shape grammar. 2 They are in two equivalent schemas: x -> div(x) and x -> x’ + x’’, where x, x’, and x’’ are triangles, quadrilaterals, or pentagons, and div(x) divides x into x’ and x’’. Sample rules are in figure 2.
Rules apply in alternative ways. Imagine a Chinese craftsman at a building site, with his tools and a trove of sticks. Shown a window opening, he starts an ice-ray. He selects a stick of the right size and inserts it between two sides of the rectangular frame to form two quadrilaterals. He continues his work by dividing one of these areas into a triangle and a pentagon. Then he divides the triangle into a triangle and a quadrilateral, and the pentagon into a quadrilateral and a pentagon. He goes on connecting sides of polygons to make others of the same kind. Everything is stable in this process, if he keeps to the rules.
It is striking how rules apply recursively, but also notice something new. Calculating in a shape grammar is visual. Rules apply directly to ice-rays. There are no hidden representations that limit what you can do — what there is, you can see, and what you see is there.
Divisions in Ice-rays may vary — some require multi-axial figures and motifs (figures 3 and 4). Just put them in rules: draw what you see before you divide, and then draw what you want. Or let the schema x -> div(x) include your rules, so that polygons are divided into two areas or more.
The Ice-rays in this exhibit were made using CNC milling. There is no end to the ice-rays you can get from the schema x -> div(x): both known ones, and ones that are new. Go on and try the schema — make an ice-ray of your own!
1. Daniel Sheets Dye, 1949, A Grammar of Chinese Lattice, Cambridge MA: Harvard University Press. 2. George Stiny, 2006, Shape: Talking About Seeing and Doing, Cambridge MA: The MIT Press.
Sponsors:
The project was funded in part by a Director’s Grant from the Council for the Arts at the Massachusetts Institute of Technology. The Council’s generous support is greatly appreciated.